Category: Coding
Points: 400
Solves: 7
Description:  ctf.crikeycon.com:43981

Enumeration

Before doing anything else on the host since we were provided with an unual port and address I attempted to ncat to it, receiving the following:

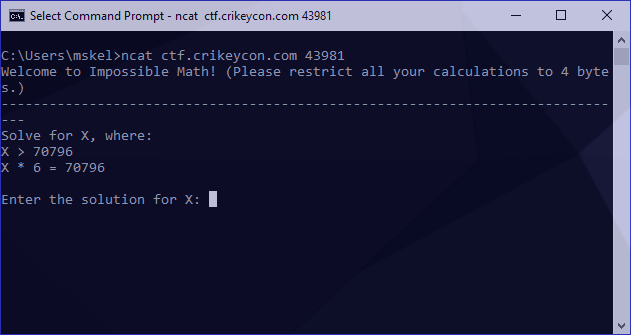
Identifying the core problem

Since the math is impossible there’s likely a trick here. With that in mind I figure we need to overload an operator (integer overflow) and try passing a large number as input:

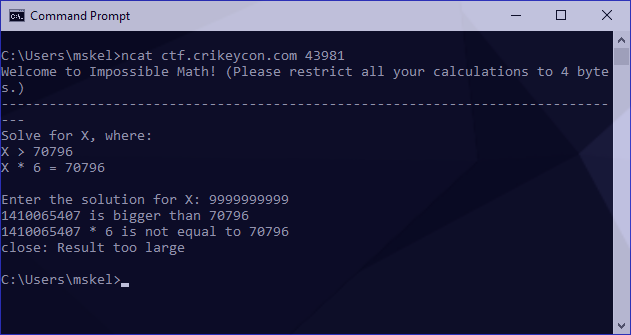
Awesome! Our integer overloads by wrapping around. To gather a bit more information I also tried an integer underflow:

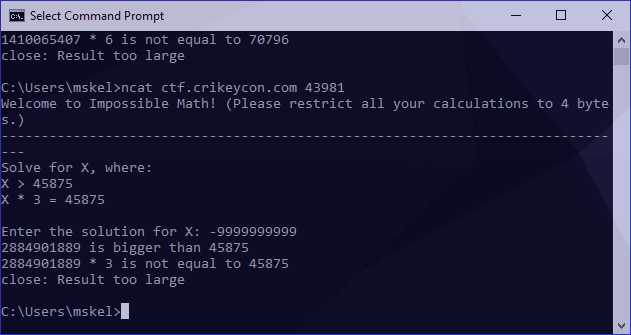
The same result. I now had to identify the figure we wrap around. These numbers are a bit irritatingly long to work with so I tried something a bit smaller to see if I could something more manageable:

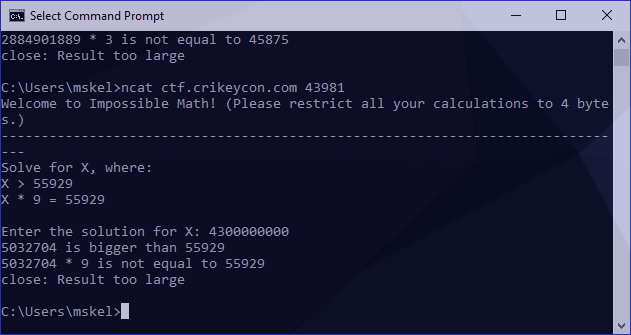
We can use the following to identify our overflow point:

4294967296 is exactly 2^32, which is 1 beyond the maximum supported by unsigned int (32 bits), further supporting our case that this is an integer overflow exercise.

To validate this, I should be able to pass this value to any problem and receive 0 back as a response (as it will reach the signed amount and loop back once), as follows:

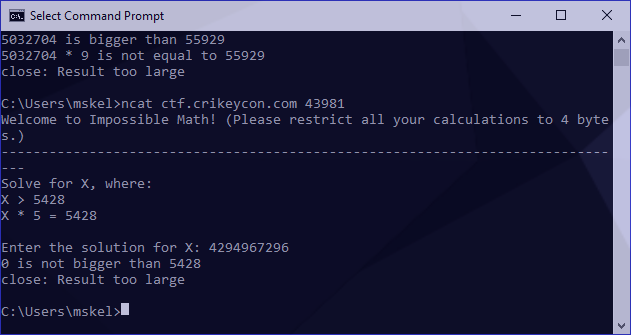
For the remainder of this exercise I’m going to refer to the variables from our second-last screenshot as the following:

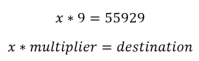
Since our number wraparounds we now know we need a number with the following conditions:

• Our overflow must be lower than 4294967296 but higher than our destination to pass the first condition.
• Our overflow needs to exceed 4294967296 when multiplied by the multiplier and result in the destination

Calculating the correct overflow

As a reminder, we can calculate our overflow using the formula from earlier:

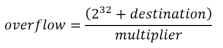
I turned this into a proof of concept by generating a new ncat session, which asked the following:

Solve for X, where:
X > 37864
X * 8 = 37864

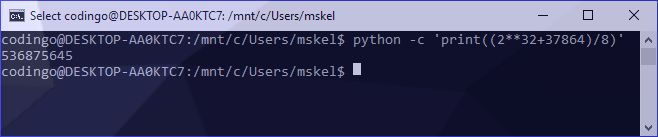
To generate our answer, I used the following:

python -c 'print((2**32+destination)/multiplier)'

This generated the answer of 536875645 as follows:

Under some circumstances, we would then be able to pipe our answer into a new ncat session but since our variables change on each connection we need to do this manually to verify it’s correct:

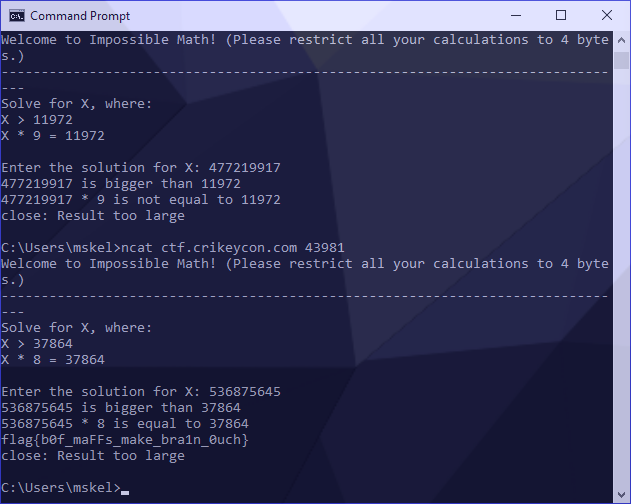
Success! Our flag was revealed.

Creating an automatic answer tool

Manual answers are great, but this is classified as a coding challenge, not a mathematical one!

There are a few core processes to this part of the exercise. First is forming an open connection and identifying our destination and multiplier from the data that comes back. We’ve also been asked in the banner of our connection to limit our calculations to 4 bytes, so we’ll make sure we limit what we request at a time.

Splitting our variables out of the calculation is quite easy. They’re both present on the line reflected as:

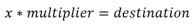
We can use regular expressions to identify this packet stream from the equals sign, and then split our values out into capture groups using another expression. Putting this boilerplate together looks like the following:

#!/usr/bin/python3
 
import socket
import re
import operator
import sys

MAXBUF = 4096
SENTINEL = 'flag'
CTF_BOT = ('ctf.crikeycon.com', 43981)


if __name__ == '__main__':
    client = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
    client.connect(CTF_BOT)

    while True:
        data = b''

        # receive and store data
        while True:
            chunk = client.recv(MAXBUF)
            data += chunk
            if len(chunk) < MAXBUF:
                break
        
        # store decoded data for future usage
        decoded = data.decode('utf-8')
        
        # print out response packet
        print(decoded)

        # our flag contains flag{}, once it's revealed print received data and exit
        if SENTINEL in decoded:
            break

        # skip loop until we see our X * Y = Z line
        if not re.search('[=]', decoded):
            continue

        # select integers and store into capture groups
        match = re.search('(\d+) = (\d+)', decoded)
   
        print('multiplier: ' + match.group(1))
        print('destination: ' + match.group(2))

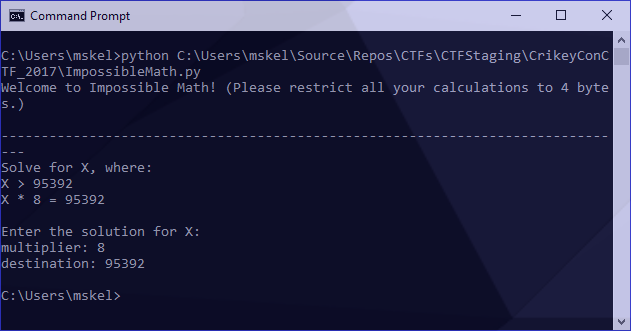
Great! We now have what we need in a variable. Referring back to our formula above, we now need to calculate:

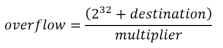
This will look like the following (note that we cast our regular expressions back to integers to prevent operand exceptions):

multiplier = int(match.group(1))
destination = int(match.group(2))
overflow = int((2**32+destination) / multiplier)

Final Script

Putting it all together we receive the following:

#!/usr/bin/python3
 
import socket
import re
import operator
import sys

MAXBUF = 4096
SENTINEL = 'flag'
CTF_BOT = ('ctf.crikeycon.com', 43981)


if __name__ == '__main__':
    client = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
    client.connect(CTF_BOT)

    while True:
        data = b''

        # receive and store data
        while True:
            chunk = client.recv(MAXBUF)
            data += chunk
            if len(chunk) < MAXBUF:
                break
        
        # store decoded data for future usage
        decoded = data.decode('utf-8')
        
        # print out response packet
        print(decoded)

        # our flag contains flag{}, once it's revealed print recevied data and exit
        if SENTINEL in decoded:
            break

        # skip loop until we see our X * Y = Z line
        if not re.search('[=]', decoded):
            continue

        # select integers and store into capture groups
        match = re.search('(\d+) = (\d+)', decoded)
   
        multiplier = int(match.group(1))
        destination = int(match.group(2))
        overflow = int((2**32+destination) / multiplier)
        
        # encode and transfer
        client.send(str(overflow).encode('utf-8')+ b'\n')

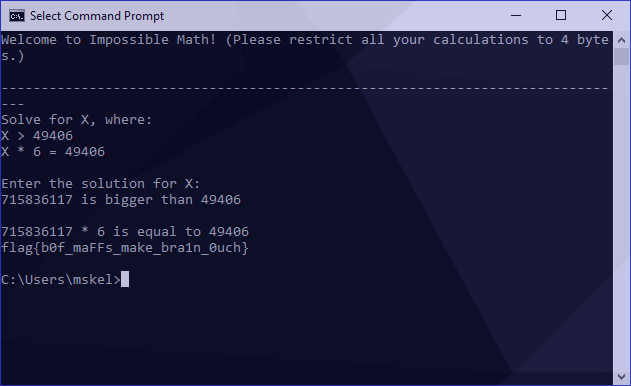
Success!

I hope this helped you to better understand integer overflows. If you’re Brisbane based, or find yourself here be sure to check out SecTalks.

• ctf
• writeup
• programming
• crikeycon